Brief Overview
We consider the problem of personalizing audio to maximize user experience. Briefly, we aim to find a filter \(h^*\), which applied to any music or speech, will maximize the user's satisfaction. This is a black-box optimization problem since the user's satisfaction function (may look as shown in the Figure below) is unknown. The key idea is to play audio samples to the user, each shaped by a different filter \(h_i\), and query the user for their satisfaction scores \(f(h_i)\). A family of ``surrogate'' functions is then designed to fit these scores and the optimization method gradually refines these functions to arrive at the filter \(\hat{h}^*\) that maximizes satisfaction. In this paper, we observe that a second type of querying is possible where users can tell us the individual elements \(h^*[j]\) of the optimal filter \(h^*\). Given a budget of \(B\) queries, where a query can be of either type, our goal is to maximize user satisfaction. Our proposal builds on Sparse Gaussian Process Regression (GPR) and shows how a hybrid approach can outperform any one type of querying. Our results are validated through simulations and real-world experiments, where volunteers gave feedback on music/speech audio and were able to achieve high satisfaction levels.

Consider the problem of personalizing content to a user's taste. Given the content \(c\), we intend to adjust the content with a linear filter \(h\). Our goal is to find the optimal filter \(h^*\) that will maximize the user's personal satisfaction \(f(h)\). Finding \(h^*\) is difficult because the user's satisfaction function \f(h)\) is unknown; it is embedded somewhere inside the perceptual regions of the brain. Hence, gradient descent is not possible since gradients cannot be computed. Black box optimization (BBO) has been proposed for such settings, where one queries user-satisfaction scores for carefully sampled \(h_i\), and from \(B\) such queries, estimate \(\hat{h}^*\) that maximizes \(\hat{f}(h)\). Of course, reducing the query budget \( B\) is of interest and the tradeoff between \(B\) and \(\hat{f}(\hat{h}^*)\) has been studied extensively.
The above problem can be called \(``\text{filter querying}''\) where the user is queried using different filters \(h_i \in R^N\). In this paper, we discuss an extension to this problem where a second type of querying is possible, called \(``\text{dimension querying}''\). With dimension querying, it is possible to query the user for each dimension of the optimal filter, namely \(h^*[1], h^*[2], \dots, h^*[N]\). In audio personalization, for example, the optimal \(h^*\) is the hearing profile of a user in the frequency domain; if we accurately estimate the hearing profile, we can maximize their satisfaction. With dimension querying, a user can listen to sound at each individual frequency \(j \in [1,N]\) and tell us the best score \(h^*[j]\). The only problem is that \(N\) can be very large, say \(8000\) Hz, hence it is prohibitive to query the user thousands of times.
To summarize, a filter query offers the advantage of understanding user satisfaction for a complete filter, while a dimension query gives optimal information for only one dimension at a time. This paper asks, for a given query budget \(B\), can the combination of two types of querying lead to higher user satisfaction compared to a single type of querying? How much is the gain from combination and how does the gain vary against various application parameters?. The Optimization problem is put formally below:
\[\text{argmin}_{\hat{h} \in \mathcal{H}} \quad ||f(\hat{h})-f(h^*)||_2\]
\[\textrm{s.t.} \quad Q_f + Q_d \leq B\]
where, \(Q_f, Q_d\) are the number of filter and dimension queries described above, and the query budget \(B \ll N\).
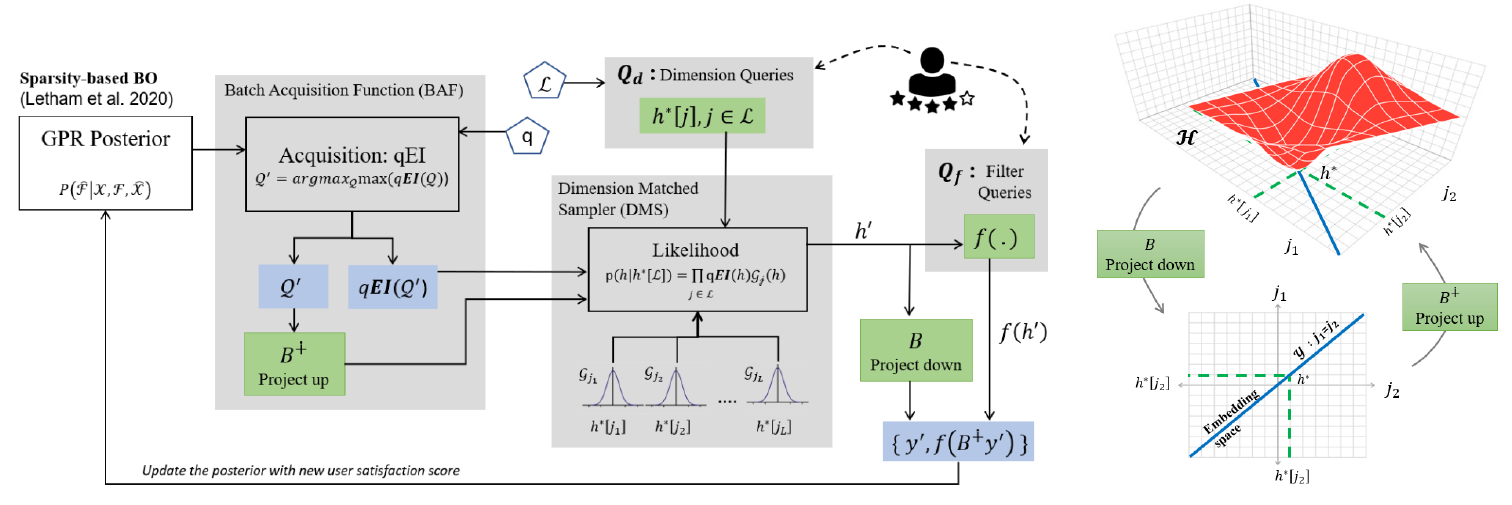
Our solution builds on past work that uses Gaussian Process Regression (GPR) as shown in the Figure below. Conventional GPR begins with a family of surrogate functions for \(f(h)\) and estimates a posterior on these functions, based on how well they satisfy the user's scores. Over time, GPR iterates through a two step process, first picking an optimal filter \(h_j\) to query the user, and based on the score \(f(h_j)\), updates the posterior distribution. The goal is to query and update posterior until a desired criteria is met. The mean of this posterior \(\hat{f}(h)\) is now declared as the surrogate for \(f(h)\) and \(\hat{h}^* = \text{argmax} \hat{f}(h)\) is announced as the final personalization filter.
The function to minimize typically, lies in a high dimensional space (i.e., \(h \in \mathcal{H} \subseteq \mathbf{R}^N, N \ge 500\)). We assume our function is sparse i.e., most dimensions do not influence \(f\) significantly, so \(f\) has ``low effective dimensions". We build upon a sparse Bayesian optimization framework to attain performance improvements independent of the sparsity technique. We use methods that exploit sparsity to create a low-dimensional embedding space using random projections, ALEBO [1]. ALEBO uses random projections to transform \(f\) to a lower dimensional embedding space such that the translation of the minimum \(h^*\) from high dimensional space \(\mathcal{H}\) to its corresponding minimum \(y^*\) in low dimensional embedding space is guaranteed. The random embedding is defined by an embedding matrix \(\mathbf{B} \in \mathbf{R}^{d \times N}\) as shown in the Figure below that transforms \(f\) into its lower dimensional equivalent \(f_B(y) = f(h) = f(\mathbf{B}^\dagger y)\). Bayesian optimization of \(f_B(y)\) is performed in the lower dimensional space \(\mathbf{R}^d\).
Synthetic Function Results
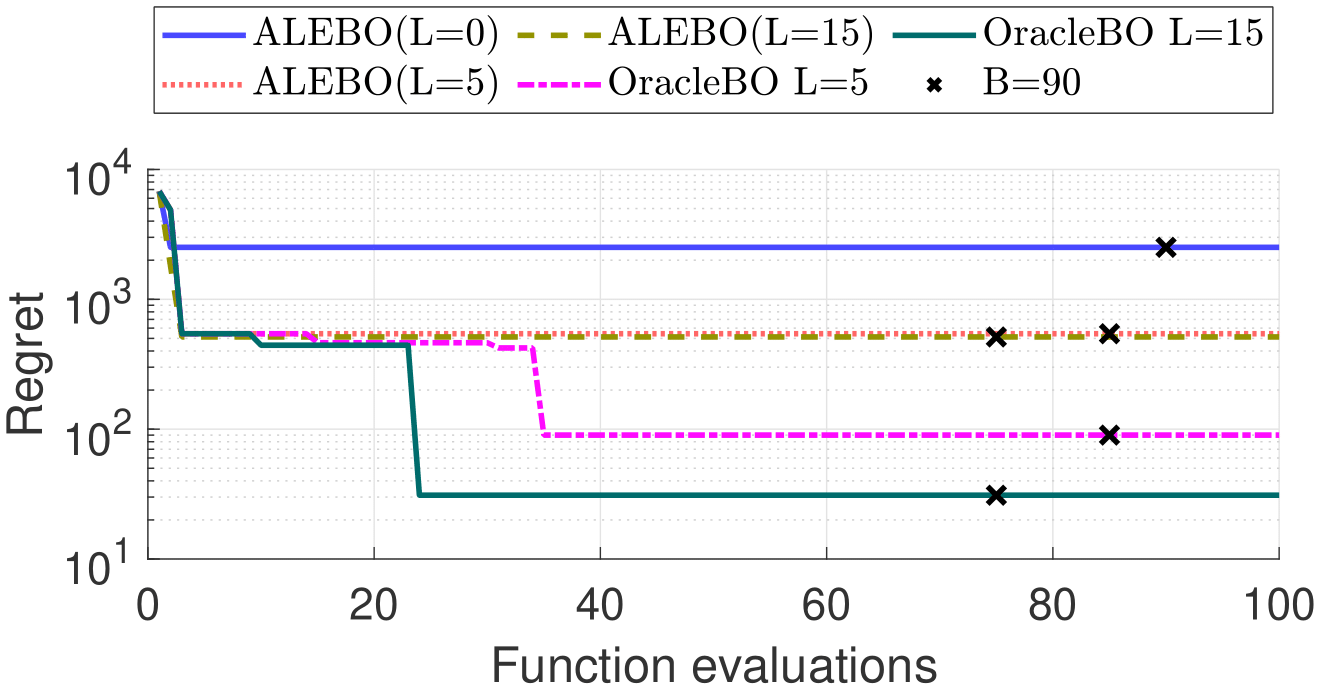
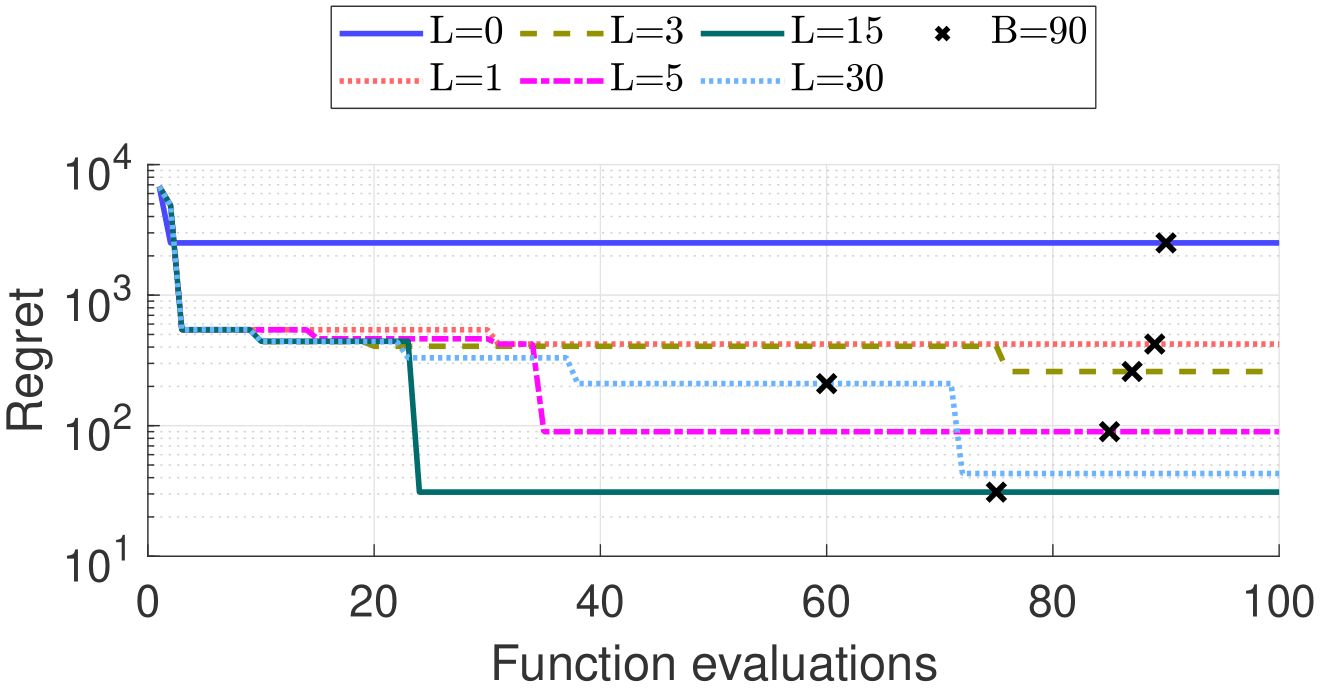
We intend to characterize the performance of OracleBO for synthetic satisfaction functions (with a staircase shape as shown in the Figure above) We compare with several baselines as follows:
- ALEBO [1] - SparseBO algorithm that only uses \(Q_f\) filter queries
- OracleBO - Our proposed algorithm that combines filter \(Q_f\) and \(Q_d\) dimension queries.
Results below show that OracleBO outperforms ALEBO and achieves better minimum \(\hat{f}_{min}\). Moreover, the performance is improved with more \(Q_d\) queries.
Audio Personalization Demo and Results
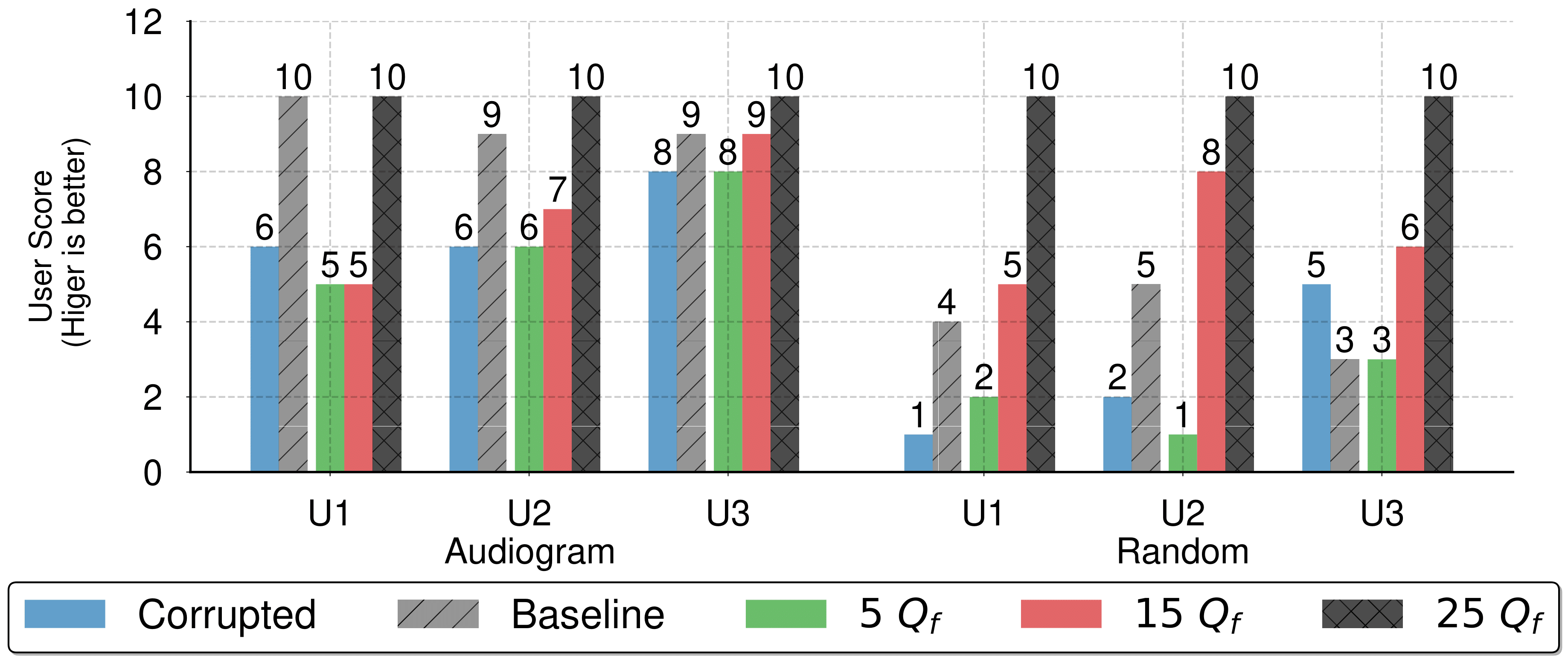
The Figure below shows the flow of operations for testing with real volunteers. We take an audio clip (Ground Truth) and first deliberately corrupt it and obtain the user satisfaction score for this clip (any other method must improve upon this score). We then analyze how a Baseline (Interpolation) filter and OracleBO improve user satisfaction through querying and user feedback.
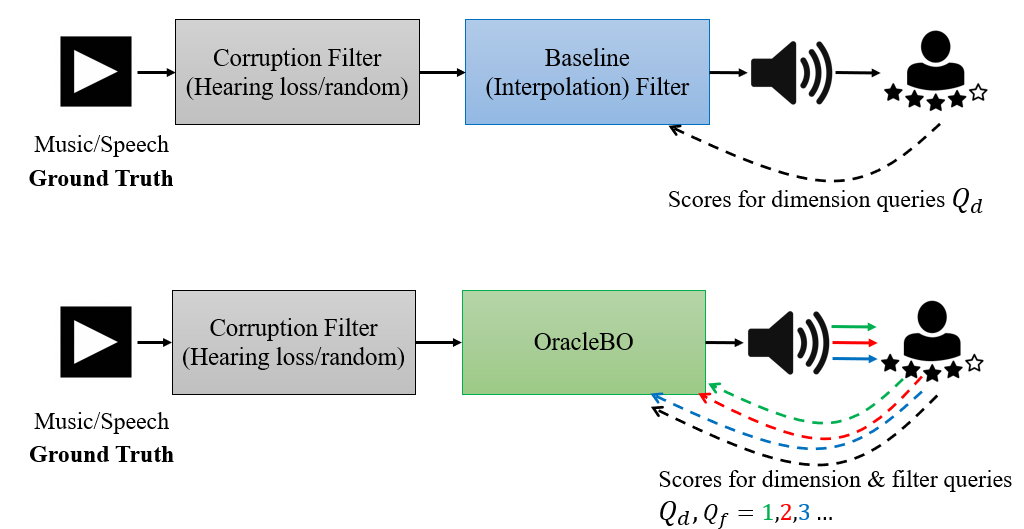
Corruption
We inject two types of corruption to the Ground Truth audio:
- We corrupt each frequency of the audio clip using a hearing loss profile from a publicly available dataset [2].
- We corrupt using a random filter which distorts each frequency independently within [-30,30] dB, i.e., \(h_r[j] \in [-30,30]{dB}, j=0,1,\dots,N\).
Baseline
Our Baseline (interpolation) filter uses dimension queries \(Q_d\). These dimension queries are essentially the user's feedback for \(Q_d\) frequency tones (typically, \(Q_d=5\) queries are measured at frequencies: \((500,1000,2000,5000,4000) Hz\)). We then interpolate this user feedback to obtain the Baseline filter. This interpolated filter is then used to compensate for the corruption (this final filter is called an ``Audiogram" when the corruption is due to hearing loss). This process (see paper for details) models how today's audio clinics configure hearing aids for each individual.
OracleBO
With OracleBO, we pretend that the user has come back home from the audio clinic with the audiogram (Baseline) filter. OracleBO now plays audio clips that are filtered with different carefully designed filters (filter queries,\(Q_f\)), and the user gives scores for these clips. Observe that this can even be done on the fly as the user listens to music or watches the news. The figure above shows the iterations with increasing filter queries (\(Q_f =\)1, 2,3 ...).
Audio Demos
The audio demo below has 2 tables: (1) the hearing loss corruption case, and (2) the random corruption case. The table columns are example audio clips heard by three different users (U1, U2, U3). The table rows indicate the following:
- Ground Truth: The original audio clip
- Corrupted: The audio clip after applying the corruption (hearing loss or random) filter.
- Baseline: The audio clip after applying the interpolation filter (from the \(Q_d=5\) dimension queries).
- OracleBO (\(Q_d=X,Q_f=Y\)): The audio clip after applying the personal filter generated by OracleBO (from querying the user \(X+Y\) times).
*Note: The audio quality you hear in the following
demos will be influenced by the frequency response of your audio-speaker, hence the quality you experience will not accurately reflect the quality perceived by users U1, U2, U3.
OracleBO is actually compensating for each user’s audio-speaker’s response function as well, hence users U1, U2, U3 should have
heard a better quality.
The Hearing Loss Corruption case
| Type | User 1 | User 2 | User 3 |
|---|---|---|---|
| Ground Truth | |||
| Corrupted | |||
| Baseline | |||
| \(Q_f=5,Q_d=5\) | |||
| \(Q_f=10,Q_d=5\) | |||
| \(Q_f=15,Q_d=5\) | |||
| \(Q_f=20,Q_d=5\) | |||
| \(Q_f=25,Q_d=5\) |
The Random Corruption case
| Type | User 1 | User 2 | User 3 |
|---|---|---|---|
| Ground Truth | |||
| Corrupted | |||
| Baseline | |||
| \(Q_f=5,Q_d=5\) | |||
| \(Q_f=10,Q_d=5\) | |||
| \(Q_f=15,Q_d=5\) | |||
| \(Q_f=20,Q_d=5\) | |||
| \(Q_f=25,Q_d=5\) |
User Satisfaction Score Results
The figure below shows the User Satisfaction Scores for (a) Hearing Loss and (b) Random filters corresponding to the Audio clips above.
References
[1] Letham, B.; Calandra, R.; Rai, A.; and Bakshy, E. 2020. Re-examining linear embeddings for high-dimensional Bayesian optimization. Advances in neural information processing systems, 33: 1546–1558
[2] NHANES CDC. 2011. Centers for Disease Control and Prevention (CDC). National Center for Health Statistics (NCHS). National Health and Nutrition Examination Survey Data, Hyattsville, MD